Il legame tra musica colta e concetti matematici è sempre stato ben più che saldo, basti pensare che negli anni ’40 del Settecento Bach ricorse alla celeberrima serie di Fibonacci nella composizione dei canoni delle Variazioni Goldberg e nel loro posizionamento all’interno delle Variazioni stesse. La serie di Fibonacci e la Sezione aurea sono state poi impiegate diffusamente come moduli costruttivi nel corso del Novecento da diversi compositori: da Debussy (La mer, Reflets dans l’eau) a Stockhausen (Klavierstücke IX) a Xenakis (Metastasis).
Un caso particolare dell’applicazione in musica di questi due concetti matematici è il compositore ungherese Béla Bartók. Difatti – come dimostrano gli studi del musicologo Ernö Lendvai – tutta l’opera di Bartók ne è pervasa, sia per quanto concerne la struttura delle composizioni sia per la sintassi armonica.
Prima di procedere è essenziale comprendere che il sistema armonico del compositore ungherese, per quanto nuovo e insolito possa sembrare alle nostre orecchie, è fondato direttamente sul sistema tonale e costituisce di questo un’evoluzione, un’espansione, come spiega così bene Enrico Minaglia nel suo studio sul balletto Il mandarino meraviglioso; e questa evoluzione prende il nome di “Sistema assiale”, all’interno del quale Bartók porta alle estreme conseguenze quel processo di superamento della semplice tonalità innescato dal Romanticismo. Eviteremo in questa sede di addentrarci nel Sistema assiale: nonostante sia estremamente affascinante e utile per la comprensione di questo straordinario compositore, richiederebbe una spiegazione fin troppo lunga che esula dai legami matematici che ci interessano.
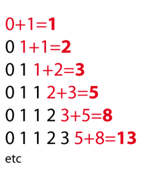
Costruzione della serie di Fibonacci
L’universo armonico di Béla Bartók, proprio come quello tonale, si divide in due rami: il sistema cromatico, basato sul principio della Sezione aurea (d’ora in poi SA), e il sistema diatonico, basato sulla serie degli armonici. Come già detto, il sistema cromatico è retto dalla SA ed essa appare nella forma della serie di Fibonacci e Bartók traduce la serie in semitoni dai quali è possibile trarre una serie di intervalli armonici caratteristici: il 2 corrisponde ad una seconda maggiore, il 3 ad una terza minore, il 5 ad una quarta giusta, e così via; inoltre questi intervalli hanno la proprietà di essere scomponibili solamente nei valori della serie stessa (es. 8=3+5). Tutto questo comporta che la mano del compositore sia obbligata a muoversi secondo un percorso rigoroso, nel quale alcune cose sono concesse e altre proibite: difatti non è possibile avere delle terze maggiori o delle seste maggiori parallele, perché corrispondono rispettivamente ai numeri 4 e 9, non presenti nella serie di Fibonacci. Addirittura Minaglia osserva che questi due intervalli «non hanno quasi mai in Bartók una forte importanza melodica», mentre le 
terze e seste minori e le seconde maggiori non solo sono molto impiegate dal compositore armonicamente, ma anche melodicamente. Lendvai osserva che Bartók, come a voler ribadire questo concetto, pone sempre la terza maggiore sotto la fondamentale e quella minore sopra di essa, usando gli intervalli 8-5-3; in questo modo si spiega la posizione del famoso accordo di maggiore-minore, nel quale la terza minore è sempre posta nella parte superiore dell’accordo.
Gli accordi maggiori-minori costruiti in questo modo sono quindi totalmente conformi alla SA perché basti sulla serie di Fibonacci e tutte le varie combinazioni armoniche devono avvenire sempre in ottemperanza a questo sistema. Inoltre, dal punto di vista melodico, Bartók si serve di tre modelli di scale differenti: «il modello 1:2, che alterna semitoni a toni interi, il modello 1:3, che alterna semitoni a terze minori, e il modello 1:5, che alterna semitoni a quarte giuste».
Dopo tutto questo viene da chiedersi in che modo la SA possa avere un proprio peso anche nel sistema diatonico, dopo aver pressoché monopolizzato il sistema cromatico. Il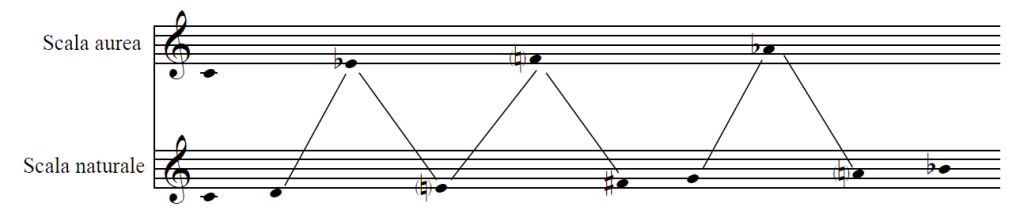 
sistema diatonico è ricavato da Bartók dagli armonici e dalla “scala” che da essi può essere desunta. Ebbene se si prende una scala costruita secondo la SA (1-3-5-8), si vedrà come essa rappresenti una sorta di negativo della scala naturale ricavata dagli armonici. Inoltre si può anche osservare come sia possibile ottenere gli intervalli tipici del sistema diatonico bartokiano semplicemente rivoltando quelli del sistema cromatico: dal 2, ossia la seconda maggiore, si ottiene la settima minore, dal 3 (terza minore) la sesta maggiore e così via.
Quali conclusioni si possono trarre da questa – seppur superficiale – analisi?
- Il sistema cromatico comprende intervalli esclusivamente dissonanti, il sistema diatonico solo quelli consonanti;
- il sistema cromatico è chiuso (ogni suono è legato contemporaneamente agli altri), quello diatonico è aperto (i suoni sono legati solo alla fondamentale).
È questo il fattore che rende così efficace la teoria musicale di Béla Bartók, il fatto che questi due “poli” siano perfettamente complementari e sovrapponibili, non solo da un punto di vista teorico ma anche per quanto concerne la stessa espressione musicale, difatti Bartók impiega il sistema cromatico quando vuole evocare coltri di tenebra e suggestioni demoniache; e quello diatonico quando vuole suggerire all’ascoltatore atmosfere assai più quiete e distese.
Come già accennato inizialmente, la serie di Fibonacci e la SA in Bartók non sono impiegate solo a livello armonico e melodico ma anche per quanto riguarda la struttura e l’organizzazione delle proprie composizioni. Un ottimo esempio di questo è il primo 
movimento della celebre Musica per archi, percussioni e celesta. Per meglio comprendere, si prenda questo “frammento” della serie di Fibonacci – 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 – e lo si compari alla struttura generale di questo movimento, che nella fattispecie è una fuga:
- battuta 1: inizio del brano, le viole espongono il soggetto della fuga;
- battuta 5: entrata della seconda voce (violini terzi e quarte);
- battuta 13: entrata della quarta voce (violini secondi);
- battuta 21: fine dell’esposizione della fuga;
- battuta 34: ingresso dei timpani, gli archi rimuovono le sordine, SA della prima parte del movimento;
- battute 55 e seguenti: grande crescendo e akme del brano, SA del movimento;
- battuta 89: fine del brano.
La cosa più stupefacente di tutto questo è che la rigorosa applicazione di tanto rigidi principî non va minimamente a discapito della musicalità di questa come di tutte le altre composizioni bartokiane. Moltissimi compositori hanno cercato di tradurre concetti matematici quali la serie di Fibonacci o le stringhe, primi fra tutti Stockhausen e Boulez, ma basterà ascoltare uno qualsiasi dei loro brani per scoprire che hanno miseramente fallito. Bartók invece no, è riuscito a coniugare perfettamente questo aspetto con la composizione perché non ha mai perso di vista il fine ultimo di un musicista e cioè fare musica, non risolvere equazioni. La musica non deve essere asservita al concetto matematico, altrimenti si giunge ai disastrosi risultati di cui si parlava prima. Un’ulteriore conferma di questo viene dall’ascolto diretto del brano di cui si è parlato: avreste mai detto che dietro di esso si celava tutto questo?
Luca Fialdini
lfmusica@yahoo.com
- Pisa celebra il “suo” Guglielmo Tell - 4 Marzo 2020
- “Don Giovanni” al Teatro Verdi di Pisa, un succès de scandale - 27 Gennaio 2020
- “Ernani” ritorna al Verdi di Pisa in cappa e spada - 17 Dicembre 2019
